Problem
(suggested by user "0ceanaut")

Find the volume of intersection of two caps within the same sphere with perpendicular base planes.

Solution
(only a plan without final calculations)

It's a typical problem on double integration. But, as in a case of the lecture on sphere's caps, I'll try to approach it using limits, though it will take some efforts. I will not present the final solution (it's a lengthy procedure), but suggest a step-by-step plan to get it.

Perpendicularity of the bases is definitely making life easier. Let's visualize the first cap to occupy a top of a sphere and have horizontal base. The second cap is positioned on the left side of a sphere with vertical base perpendicular to the first base.

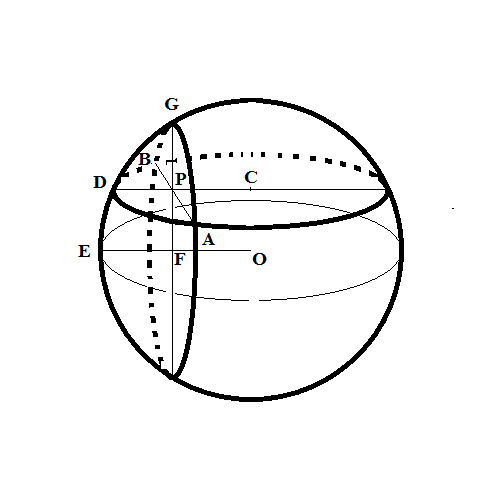
First of all, let's state the condition of two caps with heights H1 and H2 (both smaller than radius R of a sphere) and with perpendicular bases to have non-empty intersection.
It happens if the radius of one cap's base R1 (where R1²=R²−(R−H1)²) together with height of another cap H2 exceed the radius of a sphere R.
Assume now that this condition is satisfied.

Another important consideration is that the intersection between two caps with perpendicular bases is an object obtained by cutting the first cap by the plane, which is the base of the second cap. So, from the second cap we need only the base and the problem can be formulated as to find the volume of a part of a cap obtained by cutting it by a plane perpendicular to its base on certain distance from the center of that base. The distance of this cutting plane from a center of the base of the first cup is defined as R−H2, where H2 is the height of the second cap and R is the radius of a sphere.

Let point C be a center of a base of the first cap, line segment AB - line of intersection of two cap bases, CD - radius of the base of the first cap that is perpendicular to line segment AB, point P is an intersection of radius CD and line segment AB.
Let F be a center of the base of the second cap with height FE and base radius FG.

Intersection between two caps is an area inside the sphere bounded by:
part of a base of the first cap between line segment AB and its arc (a circular segment of radius CD and height PD);
part of a base of the second cap between line segment AB and its arc (a circular segment of radius FG and height PG);
surface of a sphere cut out by the two above bases.

Now let's divide a line segment PD into n equal parts by points X0=D, X1, X2, ... Xn=P.
Draw a cutting plane through each point Xk parallel to a base of a second cap (that is, perpendicular to PD). It intersects the height of the second cap at point Fk. The line FkXk lies within a cutting plane and intersects a sphere at point Yk.

This slices our object into n pieces, each slice having an almost cylindrical shape with the height (parallel to PD) equal to PD/n and a base being a circular segment (intersection of a cutting plane and the first cap) of radius FkYk and height XkYk.
We need to know the area of these circular segments to be able to calculate the volume of each slice and, later on, the sum of all volumes of slices. Then we can go to limit as n tends to infinity.

Circular segments lying on different cutting planes belong to circles of different radiuses. Let's determine the radius FkYk of a circle on a cutting plane passing through points Xk and Fk.

To determine that, let's consider a two-dimensional task obtained by cutting the sphere by a plane passing through points C (center of the first cap's base), F (center of the second cap's base) and center of a sphere O.

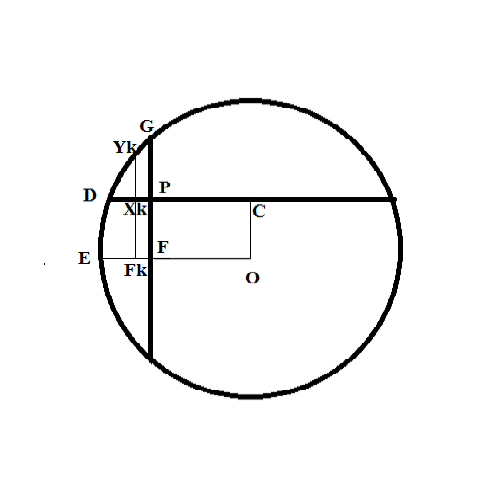
Here is the analysis:
1. Radius of a circular segment FkYk can be determined by Pythagorean Theorem, knowing OYk = R (radius of a sphere) and the length of OFk = CXk.
2. The length of CXk = CD − DXk.
3. DXk = DP·(k/n).
4. DP = CD − CP = CD − OF.
5. CD² = R² − (R−H1)².
6. OF = R − H2.
All we need now is to perform all these steps in a reversed order to get the radius FkXk and height XkYk of a circular segment we need. Then we can determine the area of this circular segment, then the volume of a k^th slice, summarize by k from 1 to n and go to limit as n→∞.

If you perform all the needed calculations, using this approach, and send it to me, I'll include the whole problem and its solution as one of Unizor problems as a menu item accessible by all people with proper attribution to you.
Thanks for suggesting this problem.